In Geometry a theorem is a statement that has to be proved deductively.

Theorems are derived from postulates and conjectures.

Unit 2

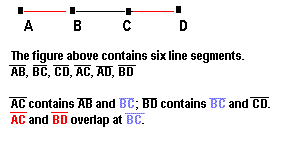
Overlapping Segments Theorem:

Given a segment with points A, B, C, and D consecutively arranged so that B and C are between A and D, the following statements are true:

1. If AB = CD, then AC = BD.

2. If AC = BD, then AB = CD.

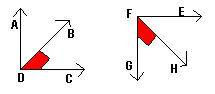
Overlapping Angles Theorem

Given <AEC with points B and C in its interior as shown, the following statements are true:

1. If m<AEB = m<CED, then m< AEC = m<BED.

2. If m<AEC = m<BED, then m<AEB = m<CED.

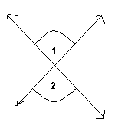
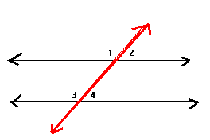
Vertical Angles Theorem

If two angles form a pair of vertical angles, then they are congruent.

<1 is congruent to <2

Reflection across two parallel lines is equivalent to a translation of twice the distance between the lines and in a direction perpendicular to the lines.

Reflection across two intersecting lines is equivalent to a rotation about the point of intersection through twice the measure of the angle between the lines.

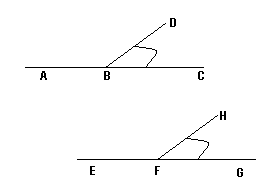
Congruent Supplements Theorem: If two angles are supplements of congruent angles, then the two angles are congruent.

<DBC is congruent to <HFG

Congruent Complements Theorem:

If two angles are complements of congruent angles, then the two angles are congruent.

<BDC is congruent to <HFG

Unit 3

The properties of a parallelogram can be proven; therefore, they are theorems.

See: Parallelogram Theorems

Write the converse of the following theorem.

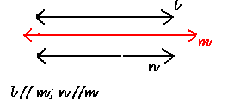
Alternate Interior Angles Theorem: If two lines cut by a transversal are parallel, then alternate interior angels are congruent.

l ¦ m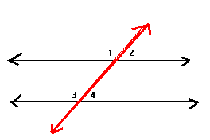

Can you list all congruent alternate interior angles and write the converse of the theorem?

Alternate exterior Angles Theorem: If two lines cut by a transversal are parallel, then alternate exterior angels are congruent.

l ¦ m

Same side Interior Angles Theorem

If two lines cut by a transversal are parallel, then same side interior angels are supplementary.

Theorem:

If two lines are parallel to the same line, then the two lines are parallel.

Given line l is parallel to line m and line n is parallel to line m. Prove line l is parallel to line n.

Triangle Sum Theorem

The sum of the measures of a triangle is 180°.

Cut the corners of the base of the triangle.

Rotate 180°. Translate the rotated figure to the apex of the triangle.

The result is a straignt angle measuring 180° Bitmap Image

Activity: Use construction paper and show that when the corner angles of the base of a triangle are cut away, rotated and translated to the apex of the triangle, then the angles form a straight angle whose measure is 180°.

Exterior Angle Theorem

The measure of an exterior angle of a triangle is equal to the sum of the measures of the remote interior angles.

Remote interior angles are those on the leg opposite the angle adjacent to the exterior angle. Bitmap Image

Sum of the exterior angles of a polygon.

The sum of the measures of the exterior angles of a polygon is 360°. This means if these angles were cut out and placed together, a circle could be formed.

Sum of the Interior Angles of a Polygon

The sum, s, of the measures of the interior angles of a polygon with n sides is given by the formula, s = (n-2)180.

Polygon	Number of sides	Number of triangular regions	Sum of interior angles
Triangle	3	1	180
Quadrilateral	4	2	360
Pentagon	5	3	540
Hexagon	6	4	720
Heptagon	7	5	900
Octagon	8	6
Nonagon	9	7	1260
Decagon		8
Dodecagon	12	10	1800
n-gon		(n-2)

Fill in the missing data.

AAS (Angle-Angle-Side) Congruence Theorem

If two angles and a nonincluded side of one triangle are congruent to the corresponding angles and nonincluded side of another triangle, then the triangles are congruent.

HL (Hypotenuse-Leg) Congruence Theorem

If the hypotenuse and a leg of a right triangle are congruent to the hypotenuse and a leg of another right triangle, then the two right triangles are congruent.

Isosceles Triangle Theorem

If two sides of a triangle are congruent, then the angles opposite those sides are congruent.

Converse of the Isosceles Triangle Theorem.

If two angles of a triangle are congruent, then the sides opposite those angles are congruent.

Equilateral triangle Corollary.

The measures of each angle of an equilateral triangle is 60 degrees.

Vertex Angle Bisector Corollary.

The bisector of the vertex angle of an isosceles triangle is the perpendicular bisector of the base.

Theorems

A diagonal of a parallelogram divides the parallelogram into two congruent triangles.

Opposite sides of a parallelogram are congruent.

Opposite angles of a parallelogram are congruent.

Consecutive angles of a parallelogram are supplementary.

The diagonals of a parallelogram bisect each other.

A rhombus is a parallelogram.

A rectangle is a parallelogram.

The diagonals of a rhombus are perpendicular (they measure 90 degrees).

The diagonals of a rectangle are congruent.

The diagonals of a kite are perpendicular.

A square is a rectangle.

A square is a rhombus.

The diagonals of a square are congruent and are the perpendicular bisectors of each other.

Theorems of quadrilaterals that are parallelograms.

If two pairs of opposite sides of a quadrilateral are congruent, then the quadrilateral is a parallelogram.

If one pair of opposite sides of a quadrilateral are parallel and congruent, then the quadrilateral is a parallelogram.

If the diagonals of a quadrilateral bisect each other, then the quadrilateral is a parallelogram.

Theorems of parallelograms that are rectangles or rhombuses.

If one angle of a parallelogram is a right angle, then the parallelogram is a rectangle.

If the diagonals of a parallelogram are congruent, then the parallelogram is a rectangle (This is known as the "House builder's Theorem".)

If one pair of adjacent sides of a parallelogram are congruent, then the parallelogram is a rhombus.

If The diagonals of a parallelogram bisect the angles of the parallelogram, then the parallelogram is a rhombus.

If the diagonals of a parallelogram are perpendicular, then the parallelogram is a rhombus.

The triangle midsegment theorem:

A midsegment of a triangle is parallel to a side of the triangle and has a measure equal to half of the measure of that side.

The center of the circumscribed circle for a right triangle is the midpoint of the hypotenuse

The midpoints of a quadrilateral are the vertices of the parallelogram.

Definition of distance.

Theorem: Sets of Parallel lines

In a perspective drawing, all lines that are parallel to each other, but not to the picture plane, meet at a single point known as the vanishing point.

Theorem: Lines Parallel to the Ground

In a perspective drawing, a line that is in the plane of the ground in the drawing and is not parallel to the picture plane will meet the horizon of the drawing at the same point.